Multimedia resources

https://www.acsysteme.com/wp-content/uploads/2021/07/control-theory-covid-Steve-Brunton-750x368.png

Automation and the COVID-19 epidemic

Home›Multimedia resources›Automation and the COVID-19 epidemic

Can we make a link between control of the COVID-19 epidemic and automation?

Steve Brunton has met this challenge brilliantly in a series of 4 instructional videos. He drew the parallel between automation theory and epidemic control strategies

The aim of automation is to find a controller which makes it possible to control the evolution of one or more variables of a system while respecting an instruction.

In the case of an epidemic:

  • the system is the epidemic,
  • the variable may be the number of people in intensive care, the number of infected people, or the number of deaths for example,
  • the instruction may be to remain below hospital capacity, minimise the number of deaths or even minimise the number of infected people,
  • the controller is all the measures taken by the government (lockdown, masks, social distancing, closing of bars and restaurants, etc.) and which we apply in varying degrees.

To design the controller and validate its operation, the automation engineer needs to model his system. Modelling an epidemic is very complex, as it involves societal and psychological concepts. Human beings have heterogeneous behaviours, which can evolve over time depending on several parameters such as the weather, for example. Also, not all viruses behave the same way.

Consequently, modelling requires making assumptions. Steve Brunton shows a comparison of several models of the evolution of the death toll as a function of time. This comparison from an article in the New York Times clearly shows that each forecast contains a relatively large margin of error and that they differ from each other (Figure 1). None of the models is perfect and their parameters are often uncertain; nevertheless, they remain very useful for designing the control strategy and evaluating its robustness.

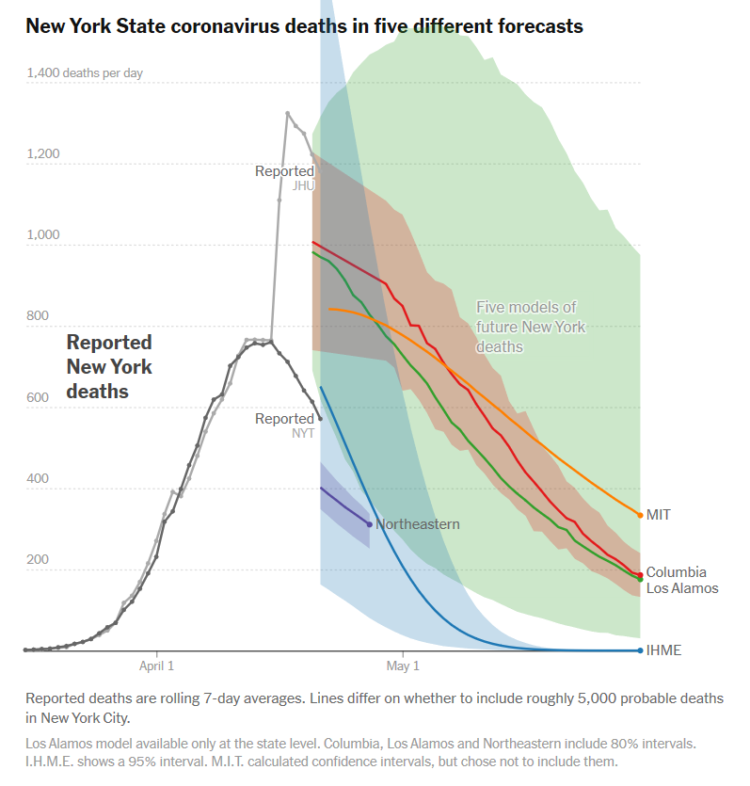
https://www.acsysteme.com/wp-content/uploads/2021/07/automatique-et-covid-750×786.png

Figure 1: 5 models which give forecasts that are very scattered and very different from each other (Graph from the article “What 5 Coronavirus Models Say the Next Month Will Look Like” written by Quoctrung Bui, Josh Katz, Alicia Parlapiano and Margot Sanger -Katz, published on 04/22/2020 on The New York Times website)

Among the major families of models quoted, compartmental models (SIR type) describe the evolution of the epidemic by differential equations. The basic reproduction number (called R0) is one of the main parameters which acts on this evolution. This number indicates the average number of people infected by a contagious person. Health measures therefore act mainly on this parameter. Another family of models is made up of statistical models which are purely mathematical and the parameters of which are identified on the basis of observations (measurements).

Once the dynamics of the epidemic evolution are understood and the model is established, it is time to think about the control strategy. It is now accepted that without a control strategy, the epidemic will grow exponentially and quickly become uncontrollable. This is a situation that most governments want to avoid. Hence the importance of adopting a control strategy.

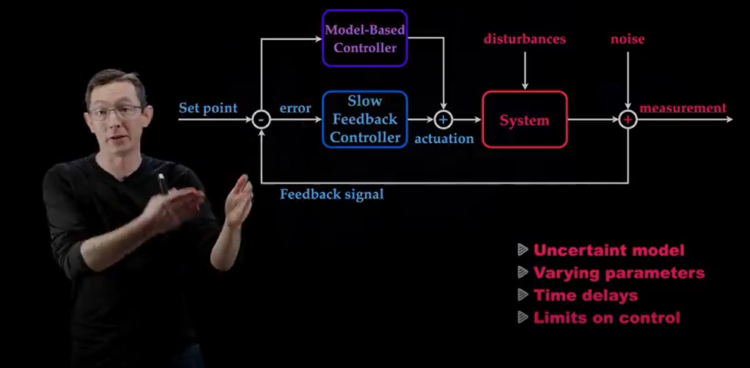
In automation, the closed loop is a classic control structure. It involves controlling a system via a controller which receives as information the error between the set point (fixed objective) and the measurement of the system variable of interest. A closed-loop control strategy would therefore be to compare the number of patients admitted to intensive care with hospital capacity and to adjust the measures (lockdown, masks, etc.) accordingly. This is the core of the automation, finding which algorithm will enable us to determine the right level of social distancing measures at the right time to reach our goal as quickly as possible whilst respecting the constraints.

The “measurement” is also very important because it will have an impact on the performance of the controller. For example, it is preferable to monitor the number of patients admitted to hospital or intensive care because the measurement is much more accurate than the number of people infected, because not everyone is tested.

The control strategy can be doomed to failure if the concept of robustness is not considered. As the model used is imperfect, as well as uncertain parameters and disturbances (climatic events, unplanned gatherings or riots) may be applied to the system. Additionally, the delays involved in COVID 19 epidemic system can severely limit robustness of control. These delays are of different natures. For example, we can quote the delay between the time when decisions are taken and the time they are applied, or the delay linked to incubation time. The development of control strategies must therefore be carried out carefully to verify that the controller stabilises the system in a safe, robust manner.

To control this type of system, Steve Brunton suggests using MPC (model predictive control). This algorithm involves predicting, via a model, the behaviour of the system over a given horizon and choosing the command which makes it possible to respect the set point over this horizon, whilst minimising the control effort. This process is repeated at each iteration. As the models are imperfect and there are delays, the MPC is coupled with a closed-loop regulator which will compare the set point with the state of the current system measured and therefore correct the command if necessary.

All the concepts and techniques covered in this series of videos are used daily by Acsystème’s engineers whose job it is to model systems and create algorithms to control them. Even if we are more used to applying them to the transportation, energy or industry fields, this article shows that the application field is much broader and can also be applied to other fields such as public health for instance.

Marouane Benaziz, june 2020

Sources:

Share this post: